BQ #7: Unit V: Derivatives and the Area Problem

Explain in detail where the formula for the difference quotient comes from now that you know. Include all appropriate terminology (secant line, tangent line, h/delta x, etc.).

The difference quotient helps us to find the slope of a tangent line at any point. But a tangent line only touches the graph once. While the secant line touches the graph twice. In order to find the slope of a secant line, we use the slope formula m = (y2-y1)/( x2-x1). So based on the first point on the graph below it is (x,f(x)) and the second point is (x+h, f(x+h)). So now we know what y2,y1,x2,x1 are. So we just plug this into the slope formula, which is m= (f(x+h))-(f(x))/((x+h)-(x)). So on the top nothing simplifies  but the bottom the 1s cancels out, which leaves us h for the denominator.

               
http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

That will give us the difference quotient: Sometimes the delta x is refer to h.


http://www.infobarrel.com/Find_the_Derivative_of_a_function_by_using_the_difference_quotient_definition








Reference:
1.)http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png
2.)http://www.infobarrel.com/Find_the_Derivative_of_a_function_by_using_the_difference_quotient_definition

BQ#6 - Unit U

1.) What is a continuity? What is a discontinuity?

A continuous function, is predictable, it has no breaks, no holes, and no jumps. It can also be drawn without lifting up your pencil from the paper. There are two types of discontinuity, which are removable and non-removable discontinuities. For removable discontinuity, which include a point discontinuity and it is also known as a HOLE. For non-removable discontinuities, which include a jump discontinuity, oscillating behavior, and an infinite discontinuity. A jump discontinuity is when it have a break or a snap. An oscillating behavior is wiggly, and an infinite discontinuity occurs when there us a vertical asymptote, which result in an unbounded behavior. 

This graph below shows a picture of a point discontinuity. Based on its intended height is 2, but the actual value is 4.
                              

http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity


The graph below shows a picture of a jump discontinuity. Where one point of the function jumps to another point.

                                       http://www.math.brown.edu/utra/discontinuities.html


The graph below shows an oscillating behavior. It is basically a wiggly graph and it's value does not exist. 

                                
                                   http://www.cwladis.com/math301/limitsgraphically.php


The picture below, shows a graph of an infinite discontinuity.

                           
                                     http://www.math.brown.edu/utra/discontinuities.html

2.) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is the intended height of a function! A limit exist when there is a continuous function or when the limit is the same as the value. A limit does not exist when there are no continuos function, or a hole. A limit is when there is an intended height of a function. The value is the actual height. 



3.)  How do we evaluate limits numerically, graphically, and algebraically?

We evaluate a limit numerically by a chart. That will allow us to find the closest value closest to a certain value we are finding. So, "as we travel a long the X-AXIS closer and closer towards a certain  value, the graph of f(x) gets closer and close to a value on the y-axis." (SSS packet)

                           https://www.nr.edu/chalmeta/271DE/Section%203.2.pdf



We evaluate graphically by graphing it on a graph. Then to see if the limit does or does not exist, we use your fingers. By putting your finger on a spot to the left of the point and to the right of the point. If your fingers meet, then there is a limit. If your fingers does not meet, then the limit does not exist.


                              
                   http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx



Finally, to evaluate the limit algebraically, we use direct substitution, rationalizing/conjugate, or dividing/factoring out method. For direct substitution, we just plug in the number that is approaching to into x. The we just simplify and we will get our answer. There are four different types of answer that we could have for direct substitution. The first one, can be a numerical answer. The second type, can be a 0 over a number, which will equal to 0. The third answer can be a number over 0, which is undefined. So, that means the limit does not exist. The fourth answer is 0 over 0, which is an indeterminate form. This means that it is NOT determined yet. So, we keep on working to figure it out.

                              

                            http://www.onlinemathlearning.com/limits-calculus.html




The next type for evaluating a limit algebraically is dividing/factoring out method. We use this type of method when we get 0/0. Which is an intermediate form, so we must use this method to find the limit. So, for this method we factor the numerator and the denominator. Then cancel out any common terms, so we could remove the zero in the denominator. Then, we have to use direct substitution with the simplified form.


                                           
                                http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm


The last type to evaluate the limit for the algebraically form is the rationalizing/conjugate method. If we tried the other two method and it does not exist, then we use this to find the limit. So, we would start off by multiplying the top and bottom by the conjugate of the top. Then we simplify the top by FOILing. Then LEAVE the non-conjugate denominator factored. So, that means we do not multiply it out. Then we eliminate, then we will get our answer.

                                      
                                     http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm



Reference:
1) SSS Packet
2.) http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity
3) http://www.math.brown.edu/utra/discontinuities.html
4) http://www.cwladis.com/math301/limitsgraphically.php
5) http://www.math.brown.edu/utra/discontinuities.html
6) http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
7) http://www.onlinemathlearning.com/limits-calculus.html
8) http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm

BQ# 4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill? Use unit Circle to explain.

Tangent is uphill, while cotangent is downhill, this is because they are opposite of each other. Based on their ratios tangent is y/x, while cotangent is x/y. Since tangent is positive it is only in the first and third quadrant. Which means that it goes up hill. 
                                 



While, cotangent is downhill because it is only positive at the first and third quadrant. At the end of the first quadrant it becomes negative. Another reason for cotangent to be negative is because it is the inverse of tangent. 

                                       

References:
http://www.nabla.hr/CO-GraphOfTransFun4.htm

BQ# 3: Unit T Concept 1-3

How do the graph of sine and cosine relate to each of the other? Emphasize asymptotes in your  response. 
1.) Tangent?

Based on the Ratio Identity, tangent equals sine/cosine. Whenever the denominator equal to 0, which means there is an asymptote. So, because cosine is the denominator, it must equal to 0, to have an asymptote.


                 


As seen in the picture below, the the tangent graph are plotted and have asymptotes. Based on the y-values are 0 for -3pi/2, -pi, pi/2, pi. etc.

                         


2.) Cotangent?

Based on the Ratio Identity, cotangent is equal to cosine/sine. So that means when sine equal to 0, there will be an asymptote. On the graph below the points that have a value of 0 are -2pi, pi, 0, pi, and 2pi.


                            


3.) Secant?

Based on the Reciprocal Identity, secant is 1/cos. The graph below shows the asymptote for secant. Which are -pi/2, pi/2, pi, 3pi/2, and 5pi/2.

                     


4.) Cosecant?

Based on the Reciprocal Identity, cosecant is equal to 1/sin. On the graph below shows the asymptote for cosecant. Which is at pi, and 2pi.

                     




References:
1.) http://www.purplemath.com/modules/triggrph3.htm
2.) http://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html

BQ# 5: Unit T Concept 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graph do? Use the Unit Circle to explain.

Sine and cosine does not have an asymptotes because based on their ratio which is y/r and x/r. The r always have to equal to 1. So both denominator for sine and cosine equal to 1. In order to have an asymptote the denominator have to equal to 0. 

However, for cosecant, secant, cotangent, and tangent they have to same ratio. For instance, like cosecant the ratio is r/y. That means the denominator has to be 0 for it to have an asymptote. While for   secant which has a ratio of r/x, the value for x have to be 0. That will give us an undefined answer, and when something is undefined = asymptote. 

BQ# 2: Unit T Concept Intro

How do the trig graph relate to the Unit Circle?
The trig graph relate to the Unit Circle, because it is the Unit Circle just need unwrapped that's
all. So it will become horizontal and correspond with the Unit Circle.
For instance, sine it is only positive in the first, and second quadrant. When you unwrap it it would be positive from 0 degrees to 180 degrees, which is 0 to pi.
For cosine, it is positive only in the first and the fourth quadrant, which is from 0 to pi/2.
For tangent, it is only positive in the first quadrant and the fourth quadrant, which is from 0 to pi/2.

Periods? -Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
The period for sine and cosine 2pi because that's so how long it takes to repeat itself. So, for sine it is +,+,-,-. For cosine it is +,-,+,-, and for tangent is +,-,+,-.


Amplitude? How does the fact that sine and cosine have amplitude of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?

Amplitude is half the distance of a period on a graph. Sine and cosine have an amplitude of 1 because based on the Unit CIrcle. That is why we cannot take the inverse of sine and cosine when it is greater than 1 or greater than -1. Other trigs does not have an amplitude because it goes on forever. Which mean that the domain is negative infinity to positive infinity. We just need to find the range.

Reflection #1: Unit Q Verifying Trig Identities

1. What does it means to verify a trig identity? 
When we are asked to verify, it means that we must prove the equation is correct. By using the trig identities. That will help us to determine that both sides equal to each other are proven to be true.

2. What tips and tricks have you found helpful?
Tips and tricks I found out helpful is to MEMORIZE the identity and the pythagorean identities. That will help us be more quicker to determine the answer. I also found out that there are many ways to prove a trig identity is true. That there not always one way we have to follow. We could either convert everything to sine and cosine, take GCF, LCD, or multiply by the conjugate. But we can NEVER EVER, touch the right side of the equation. This is because that is what we are trying it prove it to be true.

3. Explain your thought process and steps you take in verifying a trig identity.
The first thing we must do is to see if the equation can be taken out by GCF, LCD, factor, or FOIL. If this does not work, then we convert everything to sine and cosine. Then solve for the equation for what it equals to or to verify that it is true. By using the identities.

SP#7: Unit Q Concept 2: Finding All Trig Functions when given one Trig Function and Quadrant ( Using Identities)

This SP7 was made in collaboration with Daisy Larco. Please visit her awesome posts on her blog by going here.

1.) Finding all trigs by using identities.

In the first step the first thing we need to do is to see what quadrant the trig function will lie in.

So, in this case it lie in the second quadrant because that is the only place where tangent is negative and sine is positive.

The second step is to find all the trig functions by using the identities. So we know that tangent is -5/7, so we can solve for cotangent. Then we plug in the given trig for tangent and simplify to find cotangent. Once we got tangent we can solve for secant, by using 1+tan^2 theta = sec^2. Then plug in tangent and simplify to get secant. Next we solve for cosine, because we already have secant. We just need to plug in the formula cosine theta = 1/ secant theta. Then solve for cosecant, by plugging cotangent in the formula 1= cot^2 theta = csc^2 theta. That will get us cosecant. Then the only thing left we need to find is sine. Just by plugging in cosecant into the formula sin theta = 1/csc theta. This will help you find theta.

2.) Finding all trig by using SOHCAHTOA.

In order to find all the trig values, we must use SOHCAHTOA. Sine = opposite/hypotenuse, y/r. Cosine = adjacent/hypotenuse, x/r. Tangent = opposite/adjacent, y/x. Cosecant = hypotenuse/opposite, r/y. Secant = hypotenuse/adjacent, r/x. Cotangent = adjacent/opposite, x/y.

I/D #3: Unit Q - Pythagorean Identities

INQUIRY ACTIVITY SUMMARY:

1.) Where does sin^2s+cos^2x=1 come from to begin with? You should be referring to Unit Circle ratios and the Pythagorean Theorem in your explanation.
       
       a. What is an "identity"? Why is the Pythagorean Theorem an "identity"?
          An identity is a proven facts and formulas that are true. The Pythagorean Theorem is an identity because it is proven to always true.

       b. Why is the Pythagorean Theorem using x, y, and r?
         The Pythagorean Theorem uses x, y, and r because based on a right triangle in quadrant 1. It uses x, y, and r are like a, b, and c for the Pythagorean Theorem.

         


       c. Perform an operation that makes the Pythagorean Theorem equal to 1.
           We would have to divide r^2. In order to make the formula equal to 1.




      d. What is the ratio for cosine on the unit circle?
          The ratio for cosine on the unit circle is x/r. Based on SOHCAHTOA, cosine is adjacent over  hypotenuse.

           


      e. What is the ratio for sine on the unit circle?
          The same as the top one above. The ratio for sine is opposite over hypotenuse.

        

      f. What do you notice about part (c) in relation to parts (d) and (a)? What can you conclude?

   

      g. What is sin^2x+cos^2x=1 referred to as a Pythagorean Identity?
           sin^2x+cos^2x=1 is referred as the Pythagorean Identity because in order to find it we use the Pythagorean Theorem.

      h. Choose one of the "Magic 3" ordered pairs from the Unit Circle to show that this identity is true.  

          



2.) Show and explain how to derive the two remaining Pythagorean Identities from sin^2x+cos^2x=1. Be sure to show step by step.
       a. Perform a single operation fairly to derive the identity with Secant and Tangent.

         


       b. Perform a single operation fairly to derive the identity with Cosecant and Cotangent.

         



INQUIRY ACTIVITY REFLECTION:

1.) "The connection that I see between Units N, O, P, and Q so far are..."that all of them refers back to the Unit Circle. Including the Pythagorean to find all the sides. As well as find the angles by using 180º and subtracting the number we have to find the missing angles.
2.) "If I had to describe trigonometry in THREE words, they would be..." interesting but difficult. 

WPP #13-14: Unit P Concept 6&7: Applications with Law of Sines and Law of Cosines

This WPP 13-14 was made in a collaboration with Katie. Please visit the other awesome posts on her blog by going here.

Create your own Playlist on LessonPaths!

BQ#1: Unit P Concept 1 and 4: Law of Sines, Area of an Oblique Triangle, and their Derivations

1. Law of Sines 

Why do we need it?
We need the Law of Sines in order to solve for a triangle that are not right triangle. While for a right triangle we can just use the Pythagorean Theorem to find missing angles and sides. 

How is it derived and what we already know?

First lets look at a triangle, we know that it is not a right triangle because it does have a 90 degree angle label.













http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm


To make a triangle a right triangle, we must draw a line from the angle C to line AB. The red line we call it perpendicular line and label it h, now we have 2 right triangles. We know that it is a right triangle because it has a square box, which means it is 90 degree angle.

Lets recall the area of the right triangle to be Area = 1/2 base times height. To find the area of the triangle, we know that sin A = h/c and that sin c = h/a. Then we divide them the first one by c and the second by a. To get csinA = h and asinC = h.





http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm


To find angle B, we must make a perpendicular line from angle A to BC. Then use sinB = h/c and angle C is sinC = h/b. 

That will give us the formula for Law for Sines, which is: 

http://www.mathsisfun.com/algebra/trig-sine-law.ht

http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm



4. Area of an Oblique Triangle

An oblique triangle is a triangle with all sides with different length. 

How is the area of an oblique triangle derived?
Since we know that sinC = h/a, sinB = h/a, and sinA = h/c. We multiply them by their denominator and you will get:



http://wps.prenhall.com/wps/media/objects/551/564474/StudyGuide/7c1h7_1.gif

http://www.compuhigh.com/demo/lesson07_files/oblique.gif

How does it relate to the area formula that you are familiar with?
It basically uses the same formula, you just plug into the equation and find the area. We just need to use sine in order to find the height.


References:
http://www.mathsisfun.com/algebra/trig-sine-law.html
http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm
http://wps.prenhall.com/wps/media/objects/551/564474/StudyGuide/7c1h7_1.gif
http://www.compuhigh.com/demo/lesson07_files/oblique.gif

WPP#12: Unit O Concept 10: Solving Angles of Elevation and Depression Word Problems

Create your own Playlist on LessonPaths!

I/D #2: Unit O - How can we derive the patterns for our special right triangles?

Inquiry Activities Summary

1.) 30-60-90 triangle

First of all, to derive this triangle, I should start with an equilateral triangle. Which means they have all the sides equal to each other, in this case all the sides equal to 1. Not only it is equilateral but it is also equiangular, meaning the angle are the same measure as well. So for an equilateral and equiangular triangle they must add up to 180°.

First we start with a equilateral triangle, which where are the sides equal to 1.  Then split the triangle in half, which will give me a 30-60-90 triangle. Which makes the base of the triangle equal to 1/2. So, what we have already know is "a" which equal to 1/2 and is the adjacent. I also know "c," which is 1, which is the hypotenuse. In order to find "b," I must use the Pythagorean Theorem. The Pythagorean Theorem is a^2 + b^2 = c^2. Then, I plug a, and c into the Pythagorean Theorem, a = 1/2, b = ?, and c = 1, and I got 1/4 + b^2 = 1. Then subtract 1/4 and got 3/4, and then take the square root of 3/4 and got radical 3/2.

Once, I got b, which equal to radical 3/2, then I multiply 1/2, radical 3/2, and 1 by 2 to get rid of fractions. So, I would have the hypotenuse equal to 2, the opposite equal to radical 3, and the adjacent equal to 1. Next, I take "n" multiply to 1, 2, and radical 3 because "n,"shows the relationships between the three sides of the triangle.  That will give me a the derive 30-60-90 triangle.

2.) 45-45-90 Triangle

In order to derive this square into a 45-45-90, we start off with a square with all equal sides. That means the square adds up to 360° In this case which also means that the sides equal to 1. Then split the square diagonally, so it will make it a 45-45-90 triangle. So the triangle have to add up to 180°. 

Based on the triangle, I already know what "a" and "b" equals, we just need to find "c." 

So, I know that a = 1 and b = 1, to find "c," we also use the Pythagorean Theorem just like I did to find  the 30-60-90 triangle. The Pythagorean Theorem is a^2 + b^2 = c^2. So, I plug it in the formula, 1^2 + 1^2 = c^2. Then, I got 2 equal c^2, so I have to take the square root and got radical 2 for c. Then I multiply n to 1, 1, and radical 2 and got n, n, and n radical 2. That will give me a derive 45-45-90 triangle.

Inquiry Activity Reflection:

1.) "Something I never notice before about special right triangle is..."the formula was found based and it is based on the Unit Circle.

2.) "Being able to derive these patterns myself aids in my learning because..."if I happen to forget how to solve for a special right triangle I can refer back to this.

I/D #1: Unit N Concept 7: How Does SRTs and the UC relate?

Inquiry Activity summary
This activity helps us to review the rules of the special right triangle and the unit circle. As well as how they both relate to each other. There are three types of special right triangle, which are 30°, 45°, and, 60°.

1.) The first type of  right triangle is a 30°.
The shortest leg which is the opposite side of 30 and it is x.
The hypotenuse is the longest side of the triangle, which is 2x.
The side that is adjacent is y which y and has a radical of 3.
















http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html


2.) The second type of right triangle is a 45°.
The two shortest leg are both x and equal to 1.
The hypotenuse has a radical of  2.

http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html



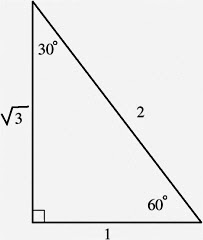
3.) The third type of right triangle is 60°.
The shortest length is x.
Whole the longest length has a radical of 3.
The hypotenuse, which is 2.

http://www.globalspec.com/reference/79218/203279/20-3-special-triangles-and-the-unit-circle

4.) This special right triangle activity helps us understand how the points make up the three types of special triangles in a unit circle.


5.) For just the information in the first quadrant we can figure out the rest.

http://www.education.com/study-help/article/unit-circle/

Based on the 30° triangle above it is positive because it is in the first quadrant. So everything will be positive and none will be negative. That is why the ordered pair, x and y will also be positive. The reference angle will be 30°. The coterminal angle will be 30°, 10°, 210°, and 330°.

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_container.html


For the 45° triangle above it is in the first quadrant so it will be positive. But if it is in the the 2nd quadrant then the x value will be negative, and the 3rd quadrant both the x and y quadrant will be negative, and the 4th quadrant only the y value will be negative. The coterminal will be 45°, 135°, 225°, and 315°.

http://www.education.com/study-help/article/unit-circle/

The 60° triangle above is in the second quadrant, so the x value will be negative. So the reference angle will be 60°. The coterminal angles are 60°, 120°, 240°, and 300°.



Inquiry Activity Reflection
1.)  The coolest thing I learned from this activity was that the specials right triangles was part of the unit circle. The special right triangle will help us to find all the points on a unit circle.

2.) This activity will helps me in this unit because I don't have to memorize all the points on the graph for the unit circle. With the help of the special right triangle I can find all the points on the unit circle.

3.) Something I never realized before about special right triangle had a big impact on the unit circle is. That is because it helps us find the ordered pairs, angles.


Reference
http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html
http://www.globalspec.com/reference/79218/203279/20-3-special-triangles-and-the-unit-circle

http://www.education.com/study-help/article/unit-circle/

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_container.html

RWA #1: Unit M Concept 5: Graphing Ellipses Given Equations and Defining All Parts

1.) The set of all points such as the sum of the distance of two points, known as the foci, is a constant. (Kirch)

2.) The standard formula of an ellipse is (x-h)^2/a^2 + (y-k)^2/b^2 = 1, for an ellipse that is fat. For a skinny ellipse the standard formula is (x-h)^2/b^2 + (y-k)^2/a^2 = 1. An ellipse is shaped like an oval. The key features of an ellipse include the standard formula, center, 2 vertices, 2 co-vertices, 2 foci,  major axis, minor axis, a, b, c and eccentricity. You can solve for all these point on an ellipse algebraically or graphically.
         By looking at the standard formula, you can find the key features algebraically. The x stands for h, and the y value stands k, this will help you finding the center (h, k). To find the major axis and minor axis, you must see if your denominator. If your denominator is bigger and is under x then the graph will be horizontally stretch, so it will be y=k. Or if the denominator is bigger under y then it will be vertically stretch, giving you x=h. You can find a and b based on your standard formula. a will always be the bigger number so you just find a^2, then you will  find a. For b is will be the smaller number so just find b^2. To find c, you must use c^2 = a^2 - b^2, then just plug in what a and b is and square rooted to find c. To find the vertices you just use a and subtracted it from the center. Whatever number that stays the same will be your major axis. For co-vertices you do the same thing you take b and subtracted it from the center. Whatever number that stays the same will be your minor axis. To find the foci you just add the number you found for c with the value that is changing. Eccentricity is the measure of how much the conic section deviates from being circular. (SSS packet) To find the eccentricity you just take  c and divide by a.
        To visualize the ellipse better, then we must graphically plot the points on the graph. The major axis is drawn with a straight line. While a minor axis is drawn with a dashed line. The vertices are the two points that lies on the two ends of the major axis. For the co-vertices the two points are on the two ends of the minor axis. If you connect all that points together will make an ellipse. To determine a, you count from the center to the major axis. For b, you count from the center to the minor axis. The foci is point within the ellipse.


This is a cool picture that determines all point of an ellipse:
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html




This video will show you how to solve and graph an ellipse:


3.)         Real world application of an ellipse can be found in elliptical orbits, in our solar system. For many years astronomers Nicholas Copernicus had discovered that the planets are orbiting the Sun, and the Moon orbits the Earth. He said that the orbits are circular. However Johannes  Kepler proved him wrong orbiting. Mars' orbit is an ellipse.
            In our solar system all of our planets have an elliptical orbits. That allow the planets to follow elliptical orbits around the Sun. The Earths' has an eccentricity of 0.01671 that is close to a circle that has an eccentricity of, 0. This shows tat the Earth is almost perfect as a circle.

4.) References
Kirch
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html
http://www.youtube.com/watch?v=5nxT6LQhXLM
http://www.as.utexas.edu/mcdonald/scope/poster/elliptical_orbits.pdf