2.) The standard formula of an ellipse is (x-h)^2/a^2 + (y-k)^2/b^2 = 1, for an ellipse that is fat. For a skinny ellipse the standard formula is (x-h)^2/b^2 + (y-k)^2/a^2 = 1. An ellipse is shaped like an oval. The key features of an ellipse include the standard formula, center, 2 vertices, 2 co-vertices, 2 foci, major axis, minor axis, a, b, c and eccentricity. You can solve for all these point on an ellipse algebraically or graphically.
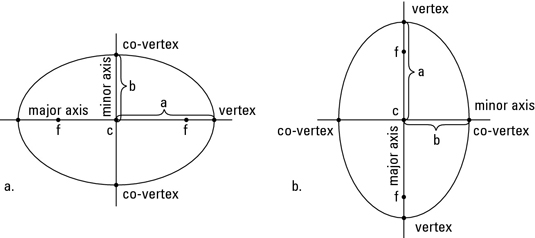
By looking at the standard formula, you can find the key features algebraically. The x stands for h, and the y value stands k, this will help you finding the center (h, k). To find the major axis and minor axis, you must see if your denominator. If your denominator is bigger and is under x then the graph will be horizontally stretch, so it will be y=k. Or if the denominator is bigger under y then it will be vertically stretch, giving you x=h. You can find a and b based on your standard formula. a will always be the bigger number so you just find a^2, then you will find a. For b is will be the smaller number so just find b^2. To find c, you must use c^2 = a^2 - b^2, then just plug in what a and b is and square rooted to find c. To find the vertices you just use a and subtracted it from the center. Whatever number that stays the same will be your major axis. For co-vertices you do the same thing you take b and subtracted it from the center. Whatever number that stays the same will be your minor axis. To find the foci you just add the number you found for c with the value that is changing. Eccentricity is the measure of how much the conic section deviates from being circular. (SSS packet) To find the eccentricity you just take c and divide by a.
To visualize the ellipse better, then we must graphically plot the points on the graph. The major axis is drawn with a straight line. While a minor axis is drawn with a dashed line. The vertices are the two points that lies on the two ends of the major axis. For the co-vertices the two points are on the two ends of the minor axis. If you connect all that points together will make an ellipse. To determine a, you count from the center to the major axis. For b, you count from the center to the minor axis. The foci is point within the ellipse.
This is a cool picture that determines all point of an ellipse:
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html
This video will show you how to solve and graph an ellipse:
3.) Real world application of an ellipse can be found in elliptical orbits, in our solar system. For many years astronomers Nicholas Copernicus had discovered that the planets are orbiting the Sun, and the Moon orbits the Earth. He said that the orbits are circular. However Johannes Kepler proved him wrong orbiting. Mars' orbit is an ellipse.
In our solar system all of our planets have an elliptical orbits. That allow the planets to follow elliptical orbits around the Sun. The Earths' has an eccentricity of 0.01671 that is close to a circle that has an eccentricity of, 0. This shows tat the Earth is almost perfect as a circle.
4.) References
Kirch
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html
http://www.youtube.com/watch?v=5nxT6LQhXLM
http://www.as.utexas.edu/mcdonald/scope/poster/elliptical_orbits.pdf
No comments:
Post a Comment