BQ #7: Unit V: Derivatives and the Area Problem

Explain in detail where the formula for the difference quotient comes from now that you know. Include all appropriate terminology (secant line, tangent line, h/delta x, etc.).

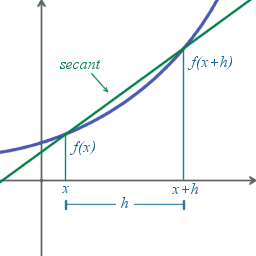
The difference quotient helps us to find the slope of a tangent line at any point. But a tangent line only touches the graph once. While the secant line touches the graph twice. In order to find the slope of a secant line, we use the slope formula m = (y2-y1)/( x2-x1). So based on the first point on the graph below it is (x,f(x)) and the second point is (x+h, f(x+h)). So now we know what y2,y1,x2,x1 are. So we just plug this into the slope formula, which is m= (f(x+h))-(f(x))/((x+h)-(x)). So on the top nothing simplifies  but the bottom the 1s cancels out, which leaves us h for the denominator.

               
http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

That will give us the difference quotient: Sometimes the delta x is refer to h.


http://www.infobarrel.com/Find_the_Derivative_of_a_function_by_using_the_difference_quotient_definition








Reference:
1.)http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png
2.)http://www.infobarrel.com/Find_the_Derivative_of_a_function_by_using_the_difference_quotient_definition

BQ#6 - Unit U

1.) What is a continuity? What is a discontinuity?

A continuous function, is predictable, it has no breaks, no holes, and no jumps. It can also be drawn without lifting up your pencil from the paper. There are two types of discontinuity, which are removable and non-removable discontinuities. For removable discontinuity, which include a point discontinuity and it is also known as a HOLE. For non-removable discontinuities, which include a jump discontinuity, oscillating behavior, and an infinite discontinuity. A jump discontinuity is when it have a break or a snap. An oscillating behavior is wiggly, and an infinite discontinuity occurs when there us a vertical asymptote, which result in an unbounded behavior. 

This graph below shows a picture of a point discontinuity. Based on its intended height is 2, but the actual value is 4.
                              

http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity


The graph below shows a picture of a jump discontinuity. Where one point of the function jumps to another point.

                                       http://www.math.brown.edu/utra/discontinuities.html


The graph below shows an oscillating behavior. It is basically a wiggly graph and it's value does not exist. 

                                
                                   http://www.cwladis.com/math301/limitsgraphically.php


The picture below, shows a graph of an infinite discontinuity.

                           
                                     http://www.math.brown.edu/utra/discontinuities.html

2.) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is the intended height of a function! A limit exist when there is a continuous function or when the limit is the same as the value. A limit does not exist when there are no continuos function, or a hole. A limit is when there is an intended height of a function. The value is the actual height. 



3.)  How do we evaluate limits numerically, graphically, and algebraically?

We evaluate a limit numerically by a chart. That will allow us to find the closest value closest to a certain value we are finding. So, "as we travel a long the X-AXIS closer and closer towards a certain  value, the graph of f(x) gets closer and close to a value on the y-axis." (SSS packet)

                           https://www.nr.edu/chalmeta/271DE/Section%203.2.pdf



We evaluate graphically by graphing it on a graph. Then to see if the limit does or does not exist, we use your fingers. By putting your finger on a spot to the left of the point and to the right of the point. If your fingers meet, then there is a limit. If your fingers does not meet, then the limit does not exist.


                              
                   http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx



Finally, to evaluate the limit algebraically, we use direct substitution, rationalizing/conjugate, or dividing/factoring out method. For direct substitution, we just plug in the number that is approaching to into x. The we just simplify and we will get our answer. There are four different types of answer that we could have for direct substitution. The first one, can be a numerical answer. The second type, can be a 0 over a number, which will equal to 0. The third answer can be a number over 0, which is undefined. So, that means the limit does not exist. The fourth answer is 0 over 0, which is an indeterminate form. This means that it is NOT determined yet. So, we keep on working to figure it out.

                              

                            http://www.onlinemathlearning.com/limits-calculus.html




The next type for evaluating a limit algebraically is dividing/factoring out method. We use this type of method when we get 0/0. Which is an intermediate form, so we must use this method to find the limit. So, for this method we factor the numerator and the denominator. Then cancel out any common terms, so we could remove the zero in the denominator. Then, we have to use direct substitution with the simplified form.


                                           
                                http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm


The last type to evaluate the limit for the algebraically form is the rationalizing/conjugate method. If we tried the other two method and it does not exist, then we use this to find the limit. So, we would start off by multiplying the top and bottom by the conjugate of the top. Then we simplify the top by FOILing. Then LEAVE the non-conjugate denominator factored. So, that means we do not multiply it out. Then we eliminate, then we will get our answer.

                                      
                                     http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm



Reference:
1) SSS Packet
2.) http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity
3) http://www.math.brown.edu/utra/discontinuities.html
4) http://www.cwladis.com/math301/limitsgraphically.php
5) http://www.math.brown.edu/utra/discontinuities.html
6) http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
7) http://www.onlinemathlearning.com/limits-calculus.html
8) http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm

BQ# 4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill? Use unit Circle to explain.

Tangent is uphill, while cotangent is downhill, this is because they are opposite of each other. Based on their ratios tangent is y/x, while cotangent is x/y. Since tangent is positive it is only in the first and third quadrant. Which means that it goes up hill. 
                                 



While, cotangent is downhill because it is only positive at the first and third quadrant. At the end of the first quadrant it becomes negative. Another reason for cotangent to be negative is because it is the inverse of tangent. 

                                       

References:
http://www.nabla.hr/CO-GraphOfTransFun4.htm

BQ# 3: Unit T Concept 1-3

How do the graph of sine and cosine relate to each of the other? Emphasize asymptotes in your  response. 
1.) Tangent?

Based on the Ratio Identity, tangent equals sine/cosine. Whenever the denominator equal to 0, which means there is an asymptote. So, because cosine is the denominator, it must equal to 0, to have an asymptote.


                 


As seen in the picture below, the the tangent graph are plotted and have asymptotes. Based on the y-values are 0 for -3pi/2, -pi, pi/2, pi. etc.

                         


2.) Cotangent?

Based on the Ratio Identity, cotangent is equal to cosine/sine. So that means when sine equal to 0, there will be an asymptote. On the graph below the points that have a value of 0 are -2pi, pi, 0, pi, and 2pi.


                            


3.) Secant?

Based on the Reciprocal Identity, secant is 1/cos. The graph below shows the asymptote for secant. Which are -pi/2, pi/2, pi, 3pi/2, and 5pi/2.

                     


4.) Cosecant?

Based on the Reciprocal Identity, cosecant is equal to 1/sin. On the graph below shows the asymptote for cosecant. Which is at pi, and 2pi.

                     




References:
1.) http://www.purplemath.com/modules/triggrph3.htm
2.) http://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html

BQ# 5: Unit T Concept 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graph do? Use the Unit Circle to explain.

Sine and cosine does not have an asymptotes because based on their ratio which is y/r and x/r. The r always have to equal to 1. So both denominator for sine and cosine equal to 1. In order to have an asymptote the denominator have to equal to 0. 

However, for cosecant, secant, cotangent, and tangent they have to same ratio. For instance, like cosecant the ratio is r/y. That means the denominator has to be 0 for it to have an asymptote. While for   secant which has a ratio of r/x, the value for x have to be 0. That will give us an undefined answer, and when something is undefined = asymptote. 

BQ# 2: Unit T Concept Intro

How do the trig graph relate to the Unit Circle?
The trig graph relate to the Unit Circle, because it is the Unit Circle just need unwrapped that's
all. So it will become horizontal and correspond with the Unit Circle.
For instance, sine it is only positive in the first, and second quadrant. When you unwrap it it would be positive from 0 degrees to 180 degrees, which is 0 to pi.
For cosine, it is positive only in the first and the fourth quadrant, which is from 0 to pi/2.
For tangent, it is only positive in the first quadrant and the fourth quadrant, which is from 0 to pi/2.

Periods? -Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
The period for sine and cosine 2pi because that's so how long it takes to repeat itself. So, for sine it is +,+,-,-. For cosine it is +,-,+,-, and for tangent is +,-,+,-.


Amplitude? How does the fact that sine and cosine have amplitude of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?

Amplitude is half the distance of a period on a graph. Sine and cosine have an amplitude of 1 because based on the Unit CIrcle. That is why we cannot take the inverse of sine and cosine when it is greater than 1 or greater than -1. Other trigs does not have an amplitude because it goes on forever. Which mean that the domain is negative infinity to positive infinity. We just need to find the range.

Reflection #1: Unit Q Verifying Trig Identities

1. What does it means to verify a trig identity? 
When we are asked to verify, it means that we must prove the equation is correct. By using the trig identities. That will help us to determine that both sides equal to each other are proven to be true.

2. What tips and tricks have you found helpful?
Tips and tricks I found out helpful is to MEMORIZE the identity and the pythagorean identities. That will help us be more quicker to determine the answer. I also found out that there are many ways to prove a trig identity is true. That there not always one way we have to follow. We could either convert everything to sine and cosine, take GCF, LCD, or multiply by the conjugate. But we can NEVER EVER, touch the right side of the equation. This is because that is what we are trying it prove it to be true.

3. Explain your thought process and steps you take in verifying a trig identity.
The first thing we must do is to see if the equation can be taken out by GCF, LCD, factor, or FOIL. If this does not work, then we convert everything to sine and cosine. Then solve for the equation for what it equals to or to verify that it is true. By using the identities.