BQ# 3: Unit T Concept 1-3

How do the graph of sine and cosine relate to each of the other? Emphasize asymptotes in your  response. 
1.) Tangent?

Based on the Ratio Identity, tangent equals sine/cosine. Whenever the denominator equal to 0, which means there is an asymptote. So, because cosine is the denominator, it must equal to 0, to have an asymptote.


                 


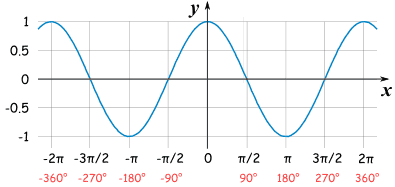
As seen in the picture below, the the tangent graph are plotted and have asymptotes. Based on the y-values are 0 for -3pi/2, -pi, pi/2, pi. etc.

                         


2.) Cotangent?

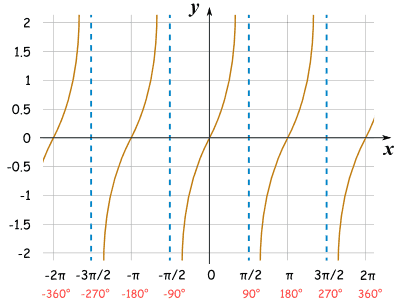
Based on the Ratio Identity, cotangent is equal to cosine/sine. So that means when sine equal to 0, there will be an asymptote. On the graph below the points that have a value of 0 are -2pi, pi, 0, pi, and 2pi.


                            


3.) Secant?

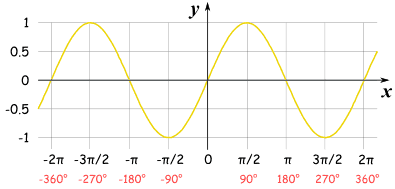
Based on the Reciprocal Identity, secant is 1/cos. The graph below shows the asymptote for secant. Which are -pi/2, pi/2, pi, 3pi/2, and 5pi/2.

                     


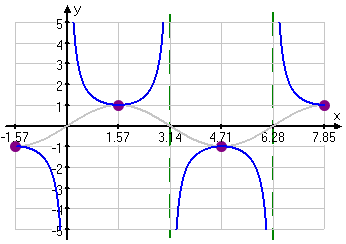
4.) Cosecant?

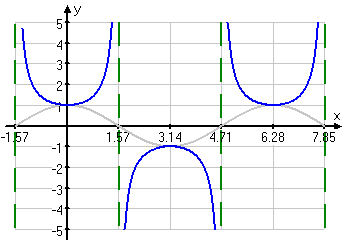
Based on the Reciprocal Identity, cosecant is equal to 1/sin. On the graph below shows the asymptote for cosecant. Which is at pi, and 2pi.

                     




References:
1.) http://www.purplemath.com/modules/triggrph3.htm
2.) http://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html