1.) What is a continuity? What is a discontinuity?
A continuous function, is predictable, it has no breaks, no holes, and no jumps. It can also be drawn without lifting up your pencil from the paper. There are two types of discontinuity, which are removable and non-removable discontinuities. For removable discontinuity, which include a point discontinuity and it is also known as a HOLE. For non-removable discontinuities, which include a jump discontinuity, oscillating behavior, and an infinite discontinuity. A jump discontinuity is when it have a break or a snap. An oscillating behavior is wiggly, and an infinite discontinuity occurs when there us a vertical asymptote, which result in an unbounded behavior.
This graph below shows a picture of a point discontinuity. Based on its intended height is 2, but the actual value is 4.
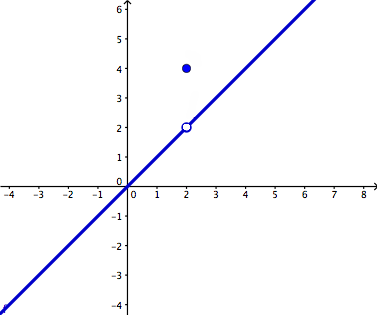
http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity
The graph below shows a picture of a jump discontinuity. Where one point of the function jumps to another point.
http://www.math.brown.edu/utra/discontinuities.html
The graph below shows an oscillating behavior. It is basically a wiggly graph and it's value does not exist.
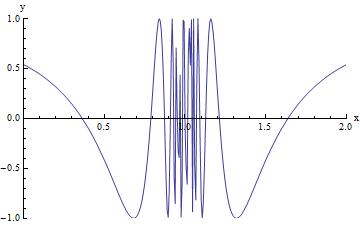
http://www.cwladis.com/math301/limitsgraphically.php
The picture below, shows a graph of an infinite discontinuity.
http://www.math.brown.edu/utra/discontinuities.html
2.) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function! A limit exist when there is a continuous function or when the limit is the same as the value. A limit does not exist when there are no continuos function, or a hole. A limit is when there is an intended height of a function. The value is the actual height.
3.) How do we evaluate limits numerically, graphically, and algebraically?
We evaluate a limit numerically by a chart. That will allow us to find the closest value closest to a certain value we are finding. So, "as we travel a long the X-AXIS closer and closer towards a certain value, the graph of f(x) gets closer and close to a value on the y-axis." (SSS packet)
https://www.nr.edu/chalmeta/271DE/Section%203.2.pdf
We evaluate graphically by graphing it on a graph. Then to see if the limit does or does not exist, we use your fingers. By putting your finger on a spot to the left of the point and to the right of the point. If your fingers meet, then there is a limit. If your fingers does not meet, then the limit does not exist.

http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
Finally, to evaluate the limit algebraically, we use direct substitution, rationalizing/conjugate, or dividing/factoring out method. For direct substitution, we just plug in the number that is approaching to into x. The we just simplify and we will get our answer. There are four different types of answer that we could have for direct substitution. The first one, can be a numerical answer. The second type, can be a 0 over a number, which will equal to 0. The third answer can be a number over 0, which is undefined. So, that means the limit does not exist. The fourth answer is 0 over 0, which is an indeterminate form. This means that it is NOT determined yet. So, we keep on working to figure it out.

The next type for evaluating a limit algebraically is dividing/factoring out method. We use this type of method when we get 0/0. Which is an intermediate form, so we must use this method to find the limit. So, for this method we factor the numerator and the denominator. Then cancel out any common terms, so we could remove the zero in the denominator. Then, we have to use direct substitution with the simplified form.

http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm
The last type to evaluate the limit for the algebraically form is the rationalizing/conjugate method. If we tried the other two method and it does not exist, then we use this to find the limit. So, we would start off by multiplying the top and bottom by the conjugate of the top. Then we simplify the top by FOILing. Then LEAVE the non-conjugate denominator factored. So, that means we do not multiply it out. Then we eliminate, then we will get our answer.
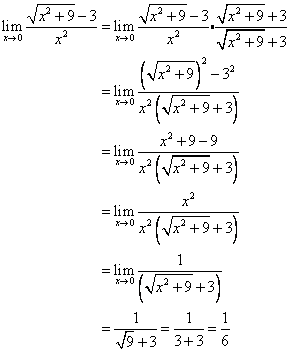
http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm
Reference:
1) SSS Packet
2.) http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity
3) http://www.math.brown.edu/utra/discontinuities.html
4) http://www.cwladis.com/math301/limitsgraphically.php
5) http://www.math.brown.edu/utra/discontinuities.html
6) http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
7) http://www.onlinemathlearning.com/limits-calculus.html
8) http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm


