I/D #1: Unit N Concept 7: How Does SRTs and the UC relate?

Inquiry Activity summary
This activity helps us to review the rules of the special right triangle and the unit circle. As well as how they both relate to each other. There are three types of special right triangle, which are 30°, 45°, and, 60°.

1.) The first type of  right triangle is a 30°.
The shortest leg which is the opposite side of 30 and it is x.
The hypotenuse is the longest side of the triangle, which is 2x.
The side that is adjacent is y which y and has a radical of 3.
















http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html


2.) The second type of right triangle is a 45°.
The two shortest leg are both x and equal to 1.
The hypotenuse has a radical of  2.

http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html



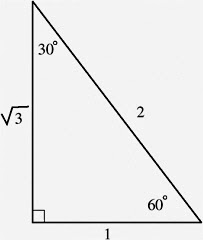
3.) The third type of right triangle is 60°.
The shortest length is x.
Whole the longest length has a radical of 3.
The hypotenuse, which is 2.

http://www.globalspec.com/reference/79218/203279/20-3-special-triangles-and-the-unit-circle

4.) This special right triangle activity helps us understand how the points make up the three types of special triangles in a unit circle.


5.) For just the information in the first quadrant we can figure out the rest.

http://www.education.com/study-help/article/unit-circle/

Based on the 30° triangle above it is positive because it is in the first quadrant. So everything will be positive and none will be negative. That is why the ordered pair, x and y will also be positive. The reference angle will be 30°. The coterminal angle will be 30°, 10°, 210°, and 330°.

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_container.html


For the 45° triangle above it is in the first quadrant so it will be positive. But if it is in the the 2nd quadrant then the x value will be negative, and the 3rd quadrant both the x and y quadrant will be negative, and the 4th quadrant only the y value will be negative. The coterminal will be 45°, 135°, 225°, and 315°.

http://www.education.com/study-help/article/unit-circle/

The 60° triangle above is in the second quadrant, so the x value will be negative. So the reference angle will be 60°. The coterminal angles are 60°, 120°, 240°, and 300°.



Inquiry Activity Reflection
1.)  The coolest thing I learned from this activity was that the specials right triangles was part of the unit circle. The special right triangle will help us to find all the points on a unit circle.

2.) This activity will helps me in this unit because I don't have to memorize all the points on the graph for the unit circle. With the help of the special right triangle I can find all the points on the unit circle.

3.) Something I never realized before about special right triangle had a big impact on the unit circle is. That is because it helps us find the ordered pairs, angles.


Reference
http://www.biology.arizona.edu/biomath/tutorials/trigonometric/specialangles.html
http://www.globalspec.com/reference/79218/203279/20-3-special-triangles-and-the-unit-circle

http://www.education.com/study-help/article/unit-circle/

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_container.html

RWA #1: Unit M Concept 5: Graphing Ellipses Given Equations and Defining All Parts

1.) The set of all points such as the sum of the distance of two points, known as the foci, is a constant. (Kirch)

2.) The standard formula of an ellipse is (x-h)^2/a^2 + (y-k)^2/b^2 = 1, for an ellipse that is fat. For a skinny ellipse the standard formula is (x-h)^2/b^2 + (y-k)^2/a^2 = 1. An ellipse is shaped like an oval. The key features of an ellipse include the standard formula, center, 2 vertices, 2 co-vertices, 2 foci,  major axis, minor axis, a, b, c and eccentricity. You can solve for all these point on an ellipse algebraically or graphically.
         By looking at the standard formula, you can find the key features algebraically. The x stands for h, and the y value stands k, this will help you finding the center (h, k). To find the major axis and minor axis, you must see if your denominator. If your denominator is bigger and is under x then the graph will be horizontally stretch, so it will be y=k. Or if the denominator is bigger under y then it will be vertically stretch, giving you x=h. You can find a and b based on your standard formula. a will always be the bigger number so you just find a^2, then you will  find a. For b is will be the smaller number so just find b^2. To find c, you must use c^2 = a^2 - b^2, then just plug in what a and b is and square rooted to find c. To find the vertices you just use a and subtracted it from the center. Whatever number that stays the same will be your major axis. For co-vertices you do the same thing you take b and subtracted it from the center. Whatever number that stays the same will be your minor axis. To find the foci you just add the number you found for c with the value that is changing. Eccentricity is the measure of how much the conic section deviates from being circular. (SSS packet) To find the eccentricity you just take  c and divide by a.
        To visualize the ellipse better, then we must graphically plot the points on the graph. The major axis is drawn with a straight line. While a minor axis is drawn with a dashed line. The vertices are the two points that lies on the two ends of the major axis. For the co-vertices the two points are on the two ends of the minor axis. If you connect all that points together will make an ellipse. To determine a, you count from the center to the major axis. For b, you count from the center to the minor axis. The foci is point within the ellipse.


This is a cool picture that determines all point of an ellipse:
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html




This video will show you how to solve and graph an ellipse:


3.)         Real world application of an ellipse can be found in elliptical orbits, in our solar system. For many years astronomers Nicholas Copernicus had discovered that the planets are orbiting the Sun, and the Moon orbits the Earth. He said that the orbits are circular. However Johannes  Kepler proved him wrong orbiting. Mars' orbit is an ellipse.
            In our solar system all of our planets have an elliptical orbits. That allow the planets to follow elliptical orbits around the Sun. The Earths' has an eccentricity of 0.01671 that is close to a circle that has an eccentricity of, 0. This shows tat the Earth is almost perfect as a circle.

4.) References
Kirch
http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html
http://www.youtube.com/watch?v=5nxT6LQhXLM
http://www.as.utexas.edu/mcdonald/scope/poster/elliptical_orbits.pdf